Authors:
(1) Cody Rucker, Department of Computer Science, University of Oregon and Corresponding author;
(2) Brittany A. Erickson, Department of Computer Science, University of Oregon and Department of Earth Sciences, University of Oregon.
Table of Links
Abstract and 1. Context and Motivation
- Physics-Informed Deep Learning Framework
- Learning Problems for Earthquakes on Rate-and-State Faults
- 2D Verification, Validation and Applications
- Summary and Future Work and References
3. Learning Problems for Earthquakes on Rate-and-State Faults
In order to best illustrate the PINN computational set-up, we begin by considering a relevant problem in 1D, in order to introduce our methodology in a simplified framework. Here we focus on the forward problem, with details of the inverse problem included in the subsequent section on the 2D application problem.
3.1. 1D Illustration
The solid Earth is governed by momentum balance and a constitutive relation defining the material rheology; in this work we assume elastic material properties. These assumptions give rise to the elastic wave equation, namely

In this work we consider rate-and-state dependent friction (RSF), an experimentallymotivated, nonlinear friction law, used in the majority of modern earthquake simulations for its ability to reproduce a wide range of observed seismic and aseismic behaviors [10, 45, 36]. In this context, the frictional strength is given by


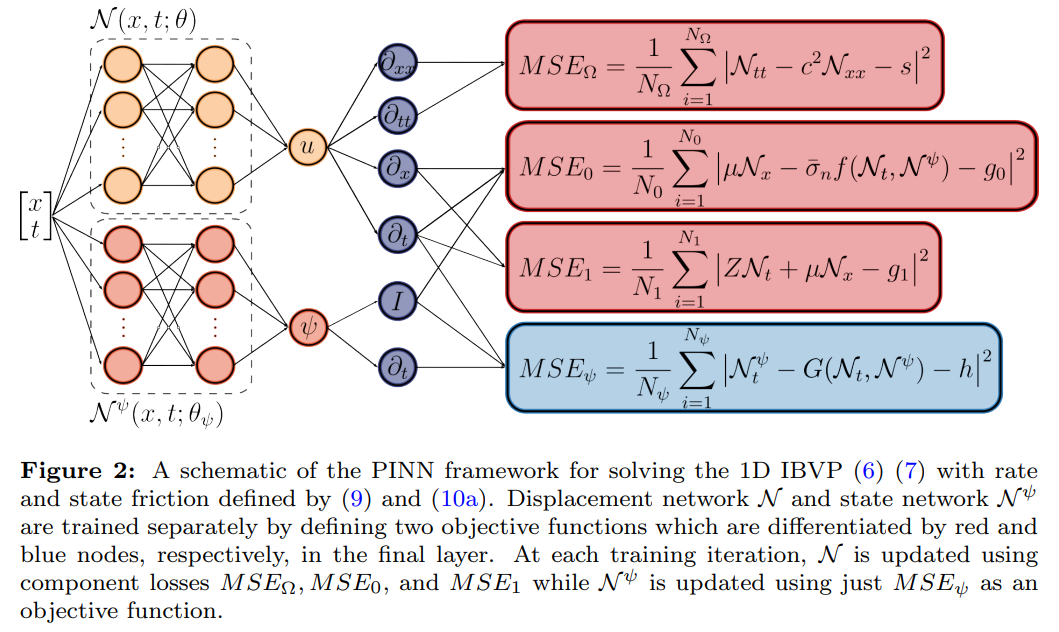
An important detail about the network training involved in minimizing the objective function MSE defined in the previous paragraph is that the inclusion of the state evolution means we are now solving a coupled system of PDE. The coupling occurs at the fault x = 0, where two conditions (fault friction (7d) and state evolution (10a)) are now enforced. Because of this coupling, the training networks N and N ψ both appear in the fault loss (11b) as well as in the state evolution loss (12a). This interconnectivity may cause training to favor accuracy in the displacement network over accuracy in the state network. In particular, high temporal variations in state evolution, variations in scale, and/or network architecture may drive the training step to favor the displacement approximation. We found it helpful to isolate the state and displacement networks during the back-propagation step. To do this, we define two objective functions: The state objective function consists of loss components in equation (12) while the displacement objective function uses loss components from equation (11). Each training iteration then requires two optimization steps to update both state and displacement networks. This setup ensures that each network is only updated by one associated objective function. We found this approach to improve our network’s training speed and resulted in better approximations of the state variable. The particulars of this training approach are illustrated in Algorithm 1 which provides the pseudocode for solving the 1D IBVP given by equations (6) and (7) where state evolves according to (10a).

This choice of manufactured solution defines the initial data u0 and v0, the source term s, and all boundary data, namely
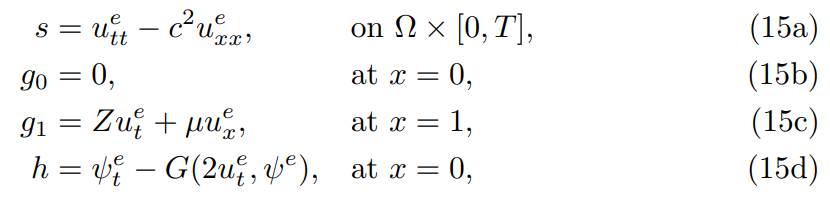
where, for the 1D problem, V (t) = 2ut(0, t), and corresponds to a commonly chosen exact solution [11, 21]
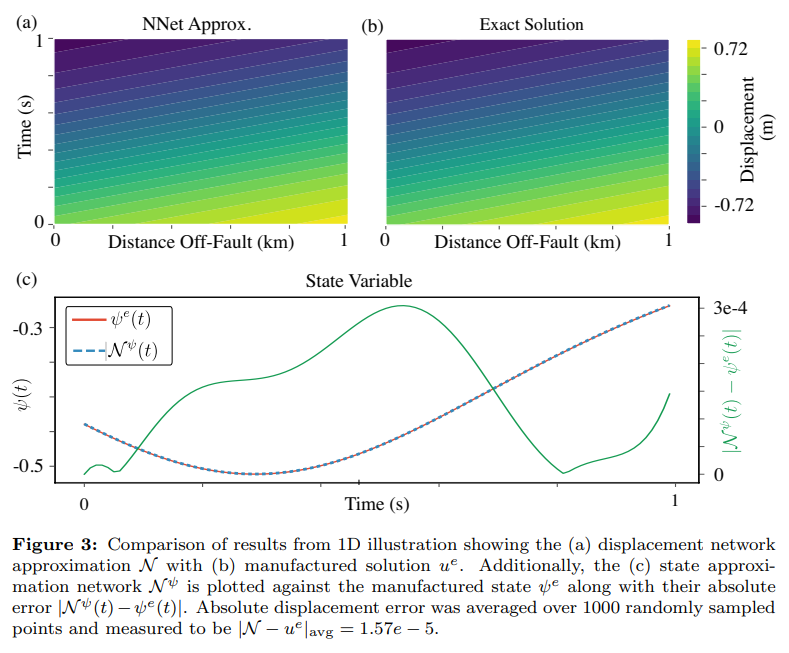
Parameter values used for all studies in this work are given in Table 1. We provide Figure 2 to illustrate how the independent networks N and N ψ are used to build each component loss function and Algorithm 1 provides an outline of the implemented code which is publicly available on GitHub [13]


3.2. 2D Application in Seismic Faulting

We assume z = 0 corresponds to Earth’s surface which we take to be traction free. An RSF vertical fault is embedded at the interface x = 0, corresponding to interface conditions


3.3. Forward and Inverse Problems for the 2D Application
Governing equation (16) along with initial and boundary conditions (17), (19) provide specifics of the loss terms (5) that define the PINN. However, there is more than one way to formulate the associated learning problem. First, one can consider either a forward or inverse problem [43]. As this work is concerned with generating approximations to both forward and inverse problems, we will refer to the primal solution as the network approximation N to the displacement u specified by the IBVP (3). The forward problem is only concerned with approximating a primal solution and requires that all model parameters λ are known a priori. A solution to the inverse problem aims to approximate the primal solution while also being tasked with learning a set of system parameters. If the λ in (3) are known, the forward problem is solved and the problem reduces to an unsupervised learning task [7]. In the inverse problem, however, the PINN has the same loss function (5) but with minor changes: Instead of knowing the system parameters λ, we establish them as trainable networks, which we detail shortly.
In addition to specifying whether a forward or inverse problem is being solved, in either case one must also choose between soft or hard enforcement of initial conditions [33, 34, 26, 7]. Soft enforcement uses loss terms to learn boundary data whereas hard enforcement encodes boundary data into a trial function to satisfy the conditions exactly. We proceed with details concerning each of these below.
3.3.1. Forward Problem
As in the 1D case, we begin by supposing that N (x, z, t; θ) ≈ u(x, z, t) for neural network N and solution u of the IBVP (16), (17), (19). The 2D component loss functions are therefore given by

3.3.2. Inverse Problem

which gives rise to the modified fault loss

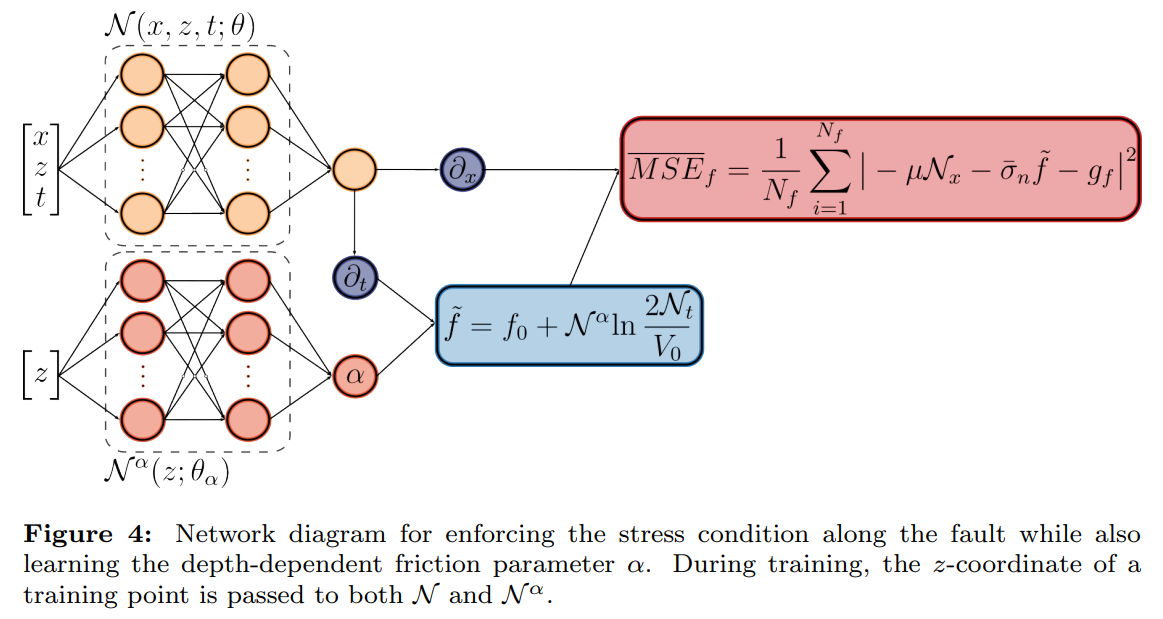
3.3.3. Soft vs. Hard Enforcement of Boundary Conditions
Both the forward and inverse problems require that we specify initial and boundary conditions, which may be enforced in two possible ways. Soft enforcement is done by penalizing the objective function, as the network output need not satisfy the condition exactly (as was done in the 1D example of the previous section). Up until now, we have presented soft enforcement, as given in

(22), which shows component losses corresponding to the boundary and initial conditions. Soft enforcement does not give us any guarantee regarding accuracy of the condition being enforced and each additional loss term in the objective function increases the complexity of the optimization landscape.

This paper is available on arxiv under CC BY 4.0 DEED license.

